By pan_g
我们认为 Hash 解决一切,自然溢出一下就好了,我直接 Hash 。
简而言之,就是通过一个映射函数 F(S) ,使得
一般来讲, F(S) = \sum_{i=0}^n B^iS_i \bmod P 或者 F(S) = \sum_{i=0}^n B^{n-i}S_i \bmod P 。
但是,由于为了更好更方便地求 Hash 值(包括一些其它的 Hash 求值),可能更倾向于后者,所以下文会按照后者计算。
有一点是非常显然的,那就是如果这个模数 P 越大,那么这个概率就越小;同样的,当 P 为质数时,在模 P 意义下得到每个数的概率可以认为是 均摊 的;还有,字符串个数 N 越大,越有可能发生 Hash 碰撞 / 冲突。
先说结论 N 个字符串发生 Hash 碰撞 / 冲突的概率是 1-e^{\frac{-N(N - 1)}{2P}} 。
因为可以考虑到如果前面已经有 i 个字符串不发生碰撞 / 冲突,只剩下 (P-i) 个位置剩余,使得不发生碰撞 / 冲突。
所以,很容易得到一个式子推一下,
再根据 Taylor 展开,
所以,根据大眼观察法,可知,
考虑到这种 Hash 方式,因为数据规模的 N 往往是被限制的。
所以简单粗暴的处理就是采用 大质数 或者 自然溢出 一下就好了 。
但是对于 这道题 来讲,因为值域的原因也很容易发生 Hash 冲突,尤其是在出题人的 良苦用心 ~~(精心构造)~~ 之下。
此时,我们就要采取 双 / 多 Hash ,这样的话 Hash 碰撞 / 冲突的发生概率是相乘的,那么此时产生这种情况的概率极小。
对于一个子串 S(l,r) 来讲,有些题可能会让我们在 O(1) 的时间内取出来,并做一定比较。
那我们就自然而然的会去想到求它的 Hash 值。
于是,去观察这个 Hash 的映射函数:
建议不要去背式子
简单抽一个 例题 ,细一看就是子串 Hash 板子,就是暴力枚举步长,再看看有几个不同的,最后取 \max 即可。
时间复杂度分析一下,
一般来讲的带修 Hash ,只是在一个子串上删一个或加一个,直接放 例题 了,思路很简单,甚至可不 Hash ,不放讲解。
那么,另一种带修 Hash 就是对字符串进行单点修改(多点就有点复杂了,因为有 Lazy Tag 的原因,不好解释),之后在进行一系列求值。
单点修改,区间查询,有结合律,无逆运算、交换律,能维护的最常见的不就是 线段树 吗?
只要记下线段树两段的长度,按类似子串 Hash 相反的方式去合并,就很轻松搞定了!
是不是肥肠简单(ε=ε=ε=┏(゜ロ゜;)┛)。
好的,看道 例题 ,也是带修 Hash 的一个套路题。
看见等差数列,同时长度 \operatorname{Len}\geq 3 ,说明我们可以直接考虑 \operatorname{Len} = 3 的情况是否满足即可,那么就可以简化一下,就是求是否存在 A_i - k 与 A_i + k 在 A_i 两侧。
于是就可以发现,出题人给的是一个 排列 ,可谓是非常 凉 心,但是排列说明了什么,说明了 值域范围是有限的 ,且 每个值只会出现一次 。
那么,考虑先把前面的数枚举一遍,考虑到只出现一次且值域为 N 的特性,可以维护一个长度为 N 的 01 串的 Hash 值, 0/1 表示值 x 是否在前面出现过。
如果对于每个 k 来讲如果都不满足条件的话,说明了以 A_i 为中心的 01 串是 回文的 ;反过来,如果对于距离 A_i 为 k 的 01 串的两个点不相等,说明了 A_i + k 或 A_i - k 其中之一没有在前面出现,然后因为每个数都会出现一遍,所以可以肯定两者是在 A_i 左右的。
于是,这道题贴一个带修 Hash 板子,判一下回文就秒掉了,是不是很简单。
我们认为你的每次出现,都是一次完美的匹配。
前缀函数的定义: P(i) 表示子串 S[0\cdots i] 最长 的 全等 的真前缀与真后缀长度,如果没有这样的真前缀与真后缀,那么为 0 。
首先,考虑暴力枚举,这个东西是 O(N^3) 。
然后,显然的我们可以考虑 从上一个的前缀 开始枚举。
为什么呢?因为如果 s[i + 1] = s[P(i)] 的话,那么此时 P(i + 1) = P(i) + 1 ,所以字符串的匹配会因为 匹配 次数,使得字符串比较次数为 O(N) ,时间复杂度 O(N^2) 。
接下来考虑 失配 的情况:
如果 s[0\cdots P(i) - 1] 与 s[i - P(i) + 1\cdots i] 是相同的,那么 s[0\cdots P(P(i) - 1)- 1] 与 s[i - P(P(i) - 1)+ 1 \cdots i] 也是相同的(其实一共是四段),见下图。
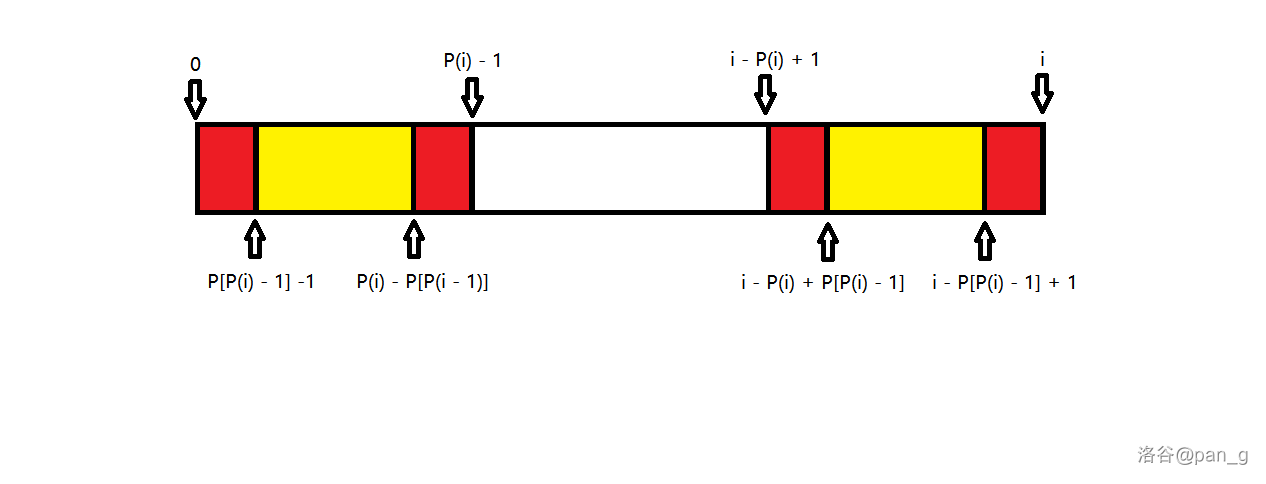
那么 P(i) 也可以是一个 失配指针 ,也就是不断地跳指针然后匹配。
时间复杂度:有一个很简单的说法,就是对于每一次求 P(i) 的操作,指针只会增加一次,所以减少也至多一次,所以时间复杂度是 O(N) 。
简称 KMP 算法,用以求模式串 s 在文本 t 中所有的 出现 。
我们可以构造一个字符串 s + \# + t ,其中 # 是一个不出现在 s 与 t 中的 脏字符 ,那么如果 P(i) = |s| ,显然就有 s 在 t 的 i - |s| + 1 - (|s| + 1) = i - 2|s| 的位置出现。
先放一道 例题 ,题意很简洁明了。
那么,就可以利用前缀函数去求这个字符串的 最小正周期 是多少。
先说结论:答案是 |s| - P(|s| - 1) ,为什么呢?
因为我们知道了 s[0\cdots P(|s| - 1)] 与 s[|s| - P(|s| - 1)\cdots |s| - 1] 是完全相等的,但是因为是真前缀的原因,并不代表 s[P(|s| - 1) + 1\cdots |s| - 1] 与 s[0\cdots |s| - P(|s| - 1) - 1] 是不完全相等的,可见下图。
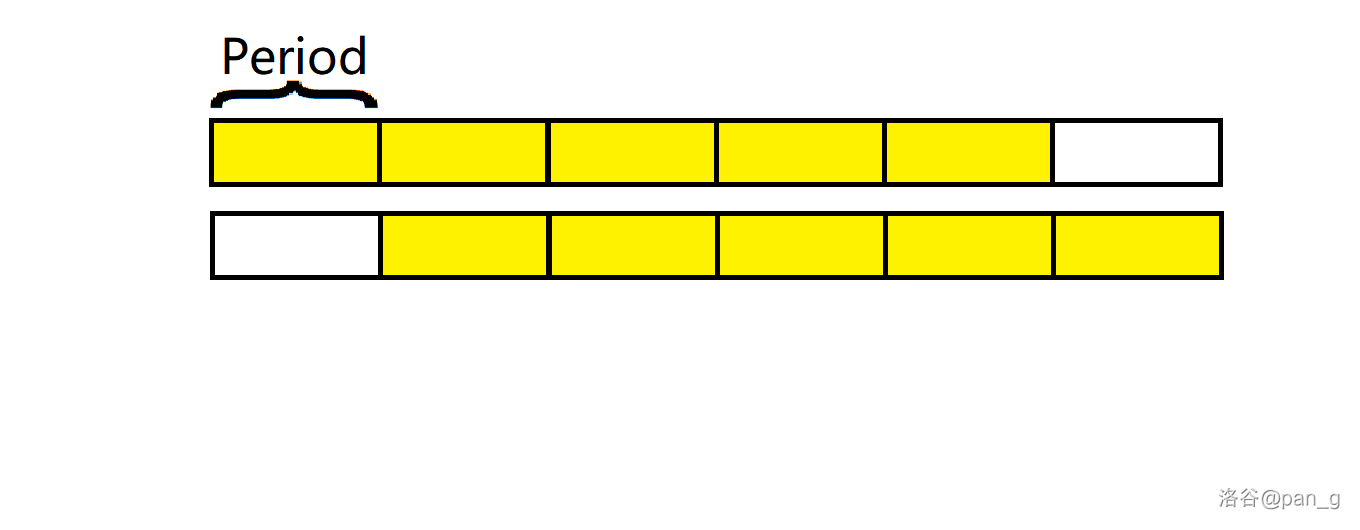
所以这就恰好说明了这一段内最小正周期就是其本身,保证了没有更小的周期存在,否则违背了 最长相同 的定义。
同样的,这一段也是这个字符串的一个周期,因为这本身就是一个周期函数,一段相等的真前缀与真后缀肯定是由 字符串的周期 构成的。
综上所述,答案就是 |s| - P(|s| - 1) 。
我们认为你的每一个巧合,都是发现相同的桥梁。
Z(x) 表示最大的满足 S[0\cdots Z(x) - 1] = S[i\cdots x + Z(x) - 1] 的值。
考虑暴力枚举,这个是 O(N ^ 2) 的。
接下来,也可以换一种想法, Hash + 二分,可以在 O(N \log N) 的复杂度内得到答案,但是依然不是最优。
我们考虑像 KMP 一样优化它,假设我已经知道了前 (x - 1) 个的 Z(x) 。
假设当前的满足 x + Z(x) - 1 最大的点为 k(k < x) ,所以 [0, Z(k) - 1] 与 [k, k + Z(k) - 1] 一定是相等的,那么考虑将 x 对应的映射点找出来,即 x - k ,就会有 [0, Z(x - k) - 1] 与 [x + Z(x - k) - 1] 相等(其实也有四段),前提是 x - k + Z(x - k) - 1 \leq Z(k) - 1 (详见下图)。
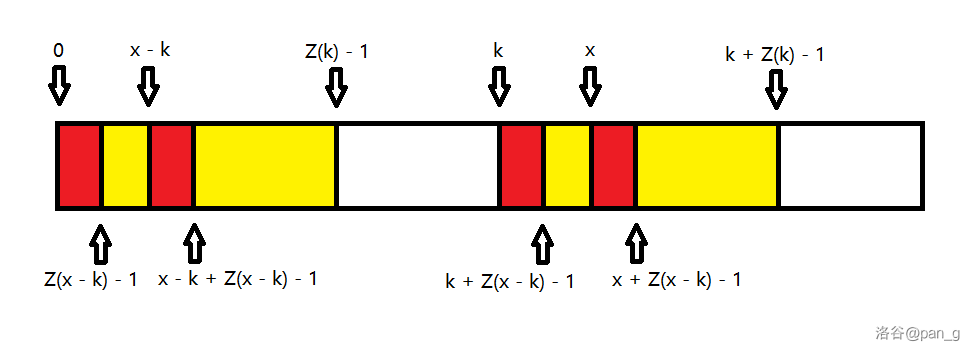
对于另一种特殊情况,即 x - k + Z(x - k) - 1 > Z(k) - 1 时,由于定义仍然有 [0, k + Z(k) - x - 1] 与 [x, k + Z(k) - 1] 相等(详见下图)。
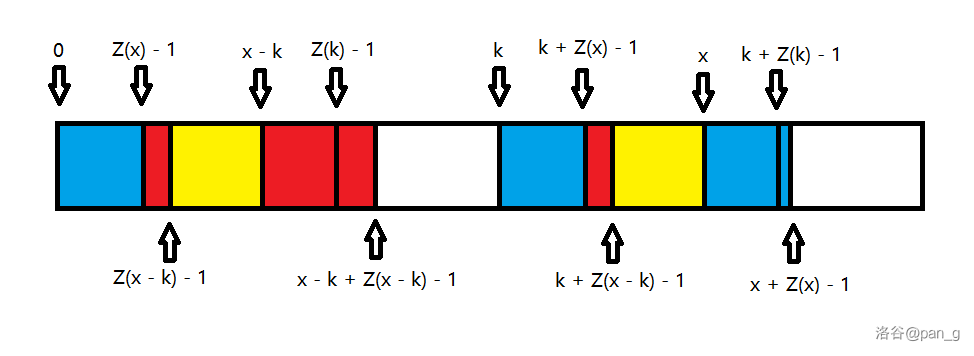
于是,由上可知 Z(x) 是在 \min\{Z(x - k), k + Z(k) - x\} 的基础上更新的,至于剩下的部分,欸?那就暴力吧。
时间复杂度:总体上来讲跟后面的 Manacher 的理念差不多(由于先写的 Manacher ),每次的暴力都会决定右端点,那么右端点最多到 N ,所以是 O(N) 的。
也称为 LCP (Longest Common Prefix) 。
求 s 与每一个 t 的后缀的 LCP 。
跟 KMP 一样,构造 s + \# + t ,跑一个 exKMP ,构造字符串中 t 对应位置的 Z(x) 就是当前位置的答案。
求 s 在 t 中的所有出现。
同上构造,如果 Z(x) = |s| ,显然就会有 s 在 t 的 x - |s| - 1 处出现。
同 KMP 处的推导,结论是最小的 |s| 的因数 d 满足 d + Z(d) = |s| ,自己悟吧,很好想的,图都是一样的。

我们认为你的每次向外拓展,都是为了下一次的便利。
现在给出一道题:
求出一个字符串 S 的最长回文子串。( |S| \leq 10^7 )
当然这道题有很多种求法,甚至用 Hash 就能把这题秒了(其实 Hash 可以做很多字符串题, Hash 不能做的基本都是你不会做的)。
比方说,你可以先处理前缀与后缀的 Hash 值,考虑到 一个回文串,去头去尾还是回文 ,所以可以先分 奇偶性 讨论,再考虑二分,然后看前后 Hash 值是否相等,总体下来时间复杂度 O(|S|\log_2|S|) 。
尽管 Hash 已经十分优秀了,但是还是秒不了这道题,于是不得不提到这个 Manacher 算法了。
其实 Manacher 和之前一样,我们可以假设已经找到了前 (i-1) 个以 j 为中心,以 R(j) 为最大半径的奇回文子串(以下未注明均是奇回文子串),接下来做的就是看是否能快速求出 R(i) ,这个回文子串也有一个优秀的性质:
假设当前的右端点最右且最长的回文子串是以 x 为中心的,那么假设有一个点 j(j < x) ,因为已经求得了 R(j) ,假设 j - R(j) + 1 \geq x - R(x) + 1 ,那么我们知道了 [j - R(j) + 1, j + R(j) - 1] 是回文的,于是又根据 [x - R(x) + 1, x + R(x) - 1] 也是回文的,且 [j - R(j) + 1, j + R(j) - 1] \subseteq [x - R(x) + 1, x + R(x) - 1] ,那么可以说明,关于 x 对称的区间 [2x - j - R(j) + 1, 2x - j + R(j) - 1] ,也是回文的(详见下图);
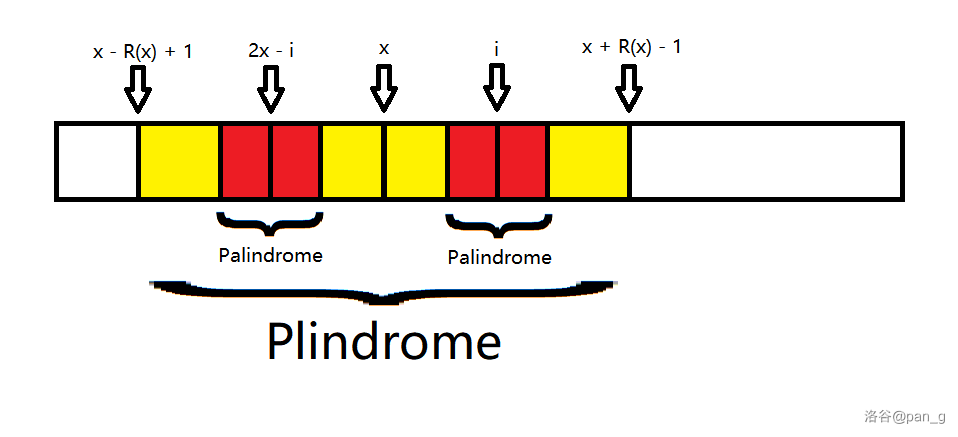
对于 j - R(j) + 1 < x - R(x) + 1 的情况,由于回文串首尾各去一个仍回文,所以假设 i 是 j 关于 x 的对称点,都有 [2i - x - R(x) + 1, x + R(x) - 1] 的区间也是回文的(详见下图)。
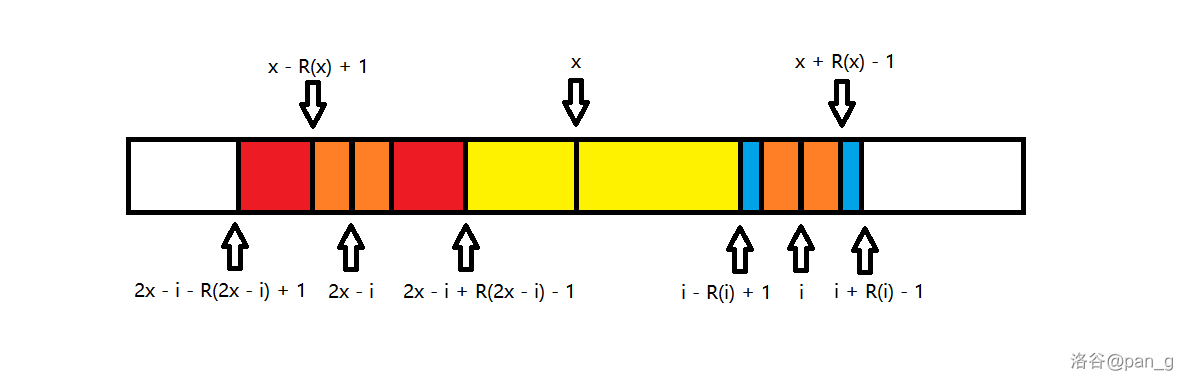
于是,由上可知 R(i) 是在 \min\{x + R(x) - i, R(2x - i)\} 的基础上更新的。
什么?剩下部分怎么办?暴力扩展呗,遇事不决就暴力。
总有人想知道,就这么一剪枝,然后就暴力,时间复杂度不会爆吗?
但是我们会注意到,当 \min 值取到 R(2x - i) 的时候,其实就已经 不会向外拓展 了,因为回文的性质,既然在左侧不回文,那么在右侧必然也不回文,否则这个当前最长串也就不是回文了。
但是取到 x + R(x) - i 时,但是取到这个 \min 时,说明这个右端点最右的最长回文子串中心 x 就有可能带来更新,那么这个右端点就会增加,但是因为不会减小的缘故,所以右端点的移动和是 O(|S|) 的。
然后整体代码枚举的复杂度,显然也是 O(|S|) 的,同上分奇偶性处理,稍加修改即可。
因为分奇偶性处理实在是太麻烦了,所以考虑合并一下两种情况。
由于上文一直再讲奇回文子串怎么处理,所以就不如全部处理成奇的。
我不禁想起了 KMP 算法的脏字符思想,于是可以在原字符串的字符中间插入一个相同的脏字符 # ,于是我们会惊奇地注意到奇回文串会以原子串中心为中心,长度为 R'(i) ;偶回文串会以一个脏字符 # 为中心,长度为 R'(i) 。
这样不仅简单化了,还少处理了很多东西。
于是这个题就可以 O(|S|) 简单地做完了。
是不是又可以 睡 一个算法了。
于是,他来了,她来了,它带着 例题 走来了。
这道例题是一个非常水的题,因为我们会了 Manacher 。
当 S 是某个串翻转之后的前缀,说明了这个串是 S 的子串,同时有一个以 S 末尾为末尾的回文串。
然后,考虑到一个字符串 s 能翻出 s' 且 s' 也能翻出 s'' 的话,那么显然 s 也是可以翻出 s'' ,所以只要找到一个能翻出一个能使自己翻出 S 前缀的字符串,那么这也是合法的。
所以,就先跑一遍 Manacher ,然后打一个标记,最后把打标记的地方全输出来即可,时间复杂度 O(|S|) 。
我们认为走自己的路,会遇见同向而行的人,但却可能分别,亦或是终结。
首先,你会得到一个 字典 ,里面有一些 单词 ,以 边 为一个 字母 ,用一条 Trie 树的 简单路径 来代表一个 单词,由于 Trie 树往往与计数问题挂钩,所以节点上往往存的是计数。
现假设有字典:
那么会有一棵前缀计数 Trie 树会长成这样(当然也可以统计很多东西):
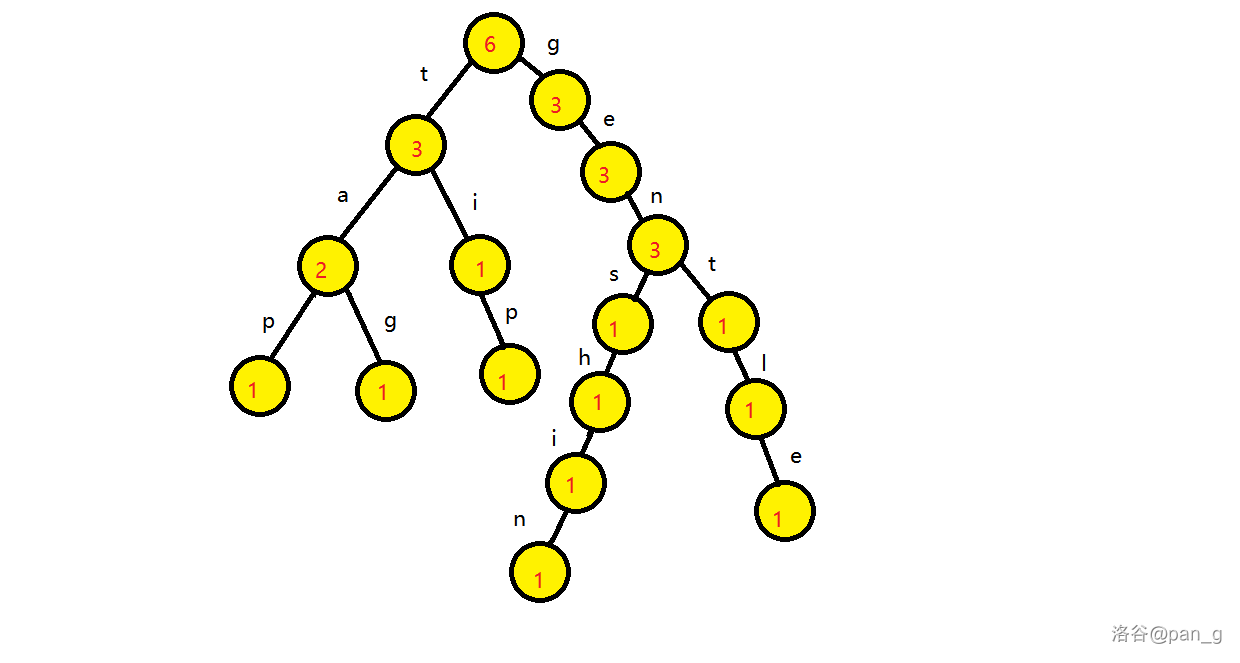
从 Trie 树的形态上来看,插入一个单词与查询一个单词的 时间复杂度与单词长度成正比,单次取 O(|S|) ,同样的 空间复杂度也是跟字典大小与单词长度呈正相关 ,这也是为什么 Trie 树容易 TLE/MLE 的原因。
看一道 板子 。
非常简单的思路,考虑建两棵单词计数 Trie ,先把原先的字典存在其中一棵中,如果不存在这棵树内,那么就是 WRONG ;再接下来,把询问的单词扔进另一棵 Trie 树内,如果已经插入了这个单词,那么就是 REPEAT ;最后,就只能是 OK 。
这是一棵 Trie 树的变体,甚至可以作为一个常数小的 计数平衡树 。
树如其名,就是树边上不再是字母或者其他东西,只有 0/1 。当然,作为一种常见的 拆位思想 ,一般也是会去解决一些有关二进制或者数的计数相关的问题。
这个思想也是非常好想到的,所以不用学也会的。
看一道处理异或极值的 问题 ,也是 Trie 树的常见应用。
首先,我们是可以处理出来每个点到节点 1 的异或路径,一遍 DFS 就好了。
注意到 自身异或的性质 a \oplus a = 0 ,于是利用这个性质,可以把有重复路径的地方给消去,所以 \operatorname{dis}(1, x) \oplus \operatorname{dis}(1, y) = \operatorname{dis}(x, y) 。
因此,我们就可以放心的把 \operatorname{dis}(1, x) 扔进 01 Trie 内,最后再一个个地查过去。
然而,因为要最大化价值,所以 01 Trie 维护的是前缀计数,尽量走与自己当前位数不同的子树,这样就可将贡献最大化。
于是就 氢悚 地把这题切了。
理论上来讲就是线段树的可持久化,类比一下就很简单了。
【暂时先挖个坑】
我们认为 AC 自动机并不能自动 AC ,和一般的观点相反,它不是很友好。
一般来讲,自动机是指 确定有限状态自动机 (Deterministic Finite Automaton, DFA) 。
是 Automaton ,不是 Automation 啊喂!
由字符集 \Sigma ,状态集合 Q ,起始状态 S \in Q ,接受状态集合 F \subseteq Q ,与状态转移函数 \delta(q, \sigma), q \in Q, \sigma \in \Sigma 构成的五元组就是自动机,可以转化为一张图,比如 Trie 树就是一个自动机,甚至还会有 KMP 自动机之类的。
此处仅做了解并相应的采用其中的一些概念,更多请移步其它网站或博客。
AC 自动机主要解决了一个多模式串匹配的问题。
分为 Trie 树与 fail 指针两部分,即 KMP 的失配指针。
我们将所有的模式串扔进一个 Trie 树内部,就把 AC 自动机完成了一半。
失配指针与 KMP 的是差不多的,但是它是可以跳到别的字符串上,当然也会跳到自己本身。
接下来,我们将失配指针称为 \operatorname{fail} 指针。
令状态 u = \delta(p, c) \in Q, p \in Q, c \in \Sigma 表示 u 是 p 通过 c 字符相连的孩子。
\operatorname{fail}(u) 指向的 v 满足 v \in Q 且 v 是 u 的最长后缀。
可以发现, \operatorname{fail}(S) = S 。
类比 KMP ,如果 \delta(\operatorname{fail}(p), c) \in Q 那么,就一定有 \operatorname{fail}(u) = \delta(\operatorname{fail}(p), c) ,否则就找 \delta(\operatorname{fail}(\operatorname{fail}(p)), c) 依此类推。
比如,现借一下 OI-Wiki 的例子,有模式串:
那么,最后的 AC 自动机会长成这样:
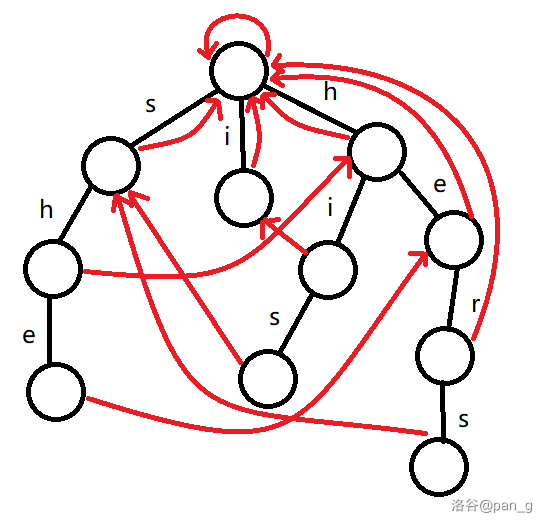
看起来好阔怕,不想学了 ~~
可以采用 BFS 的方式,假设深度比状态 u 小的 \operatorname{fail} 指针的构建都已完成。
那么我们有如下构造:
如果 \delta(u, c) \in Q 那么,就将 \operatorname{fail}(\delta(u, c)) \leftarrow \delta(\operatorname{fail}(u), c) ,否则就将 \delta(u, c) \leftarrow \delta(\operatorname{fail}(u), c) 。
这样就可以保证在文本串没有对应节点时的匹配,自然跳到 \operatorname{fail} 指针处。
所以实际上是会长成这样:
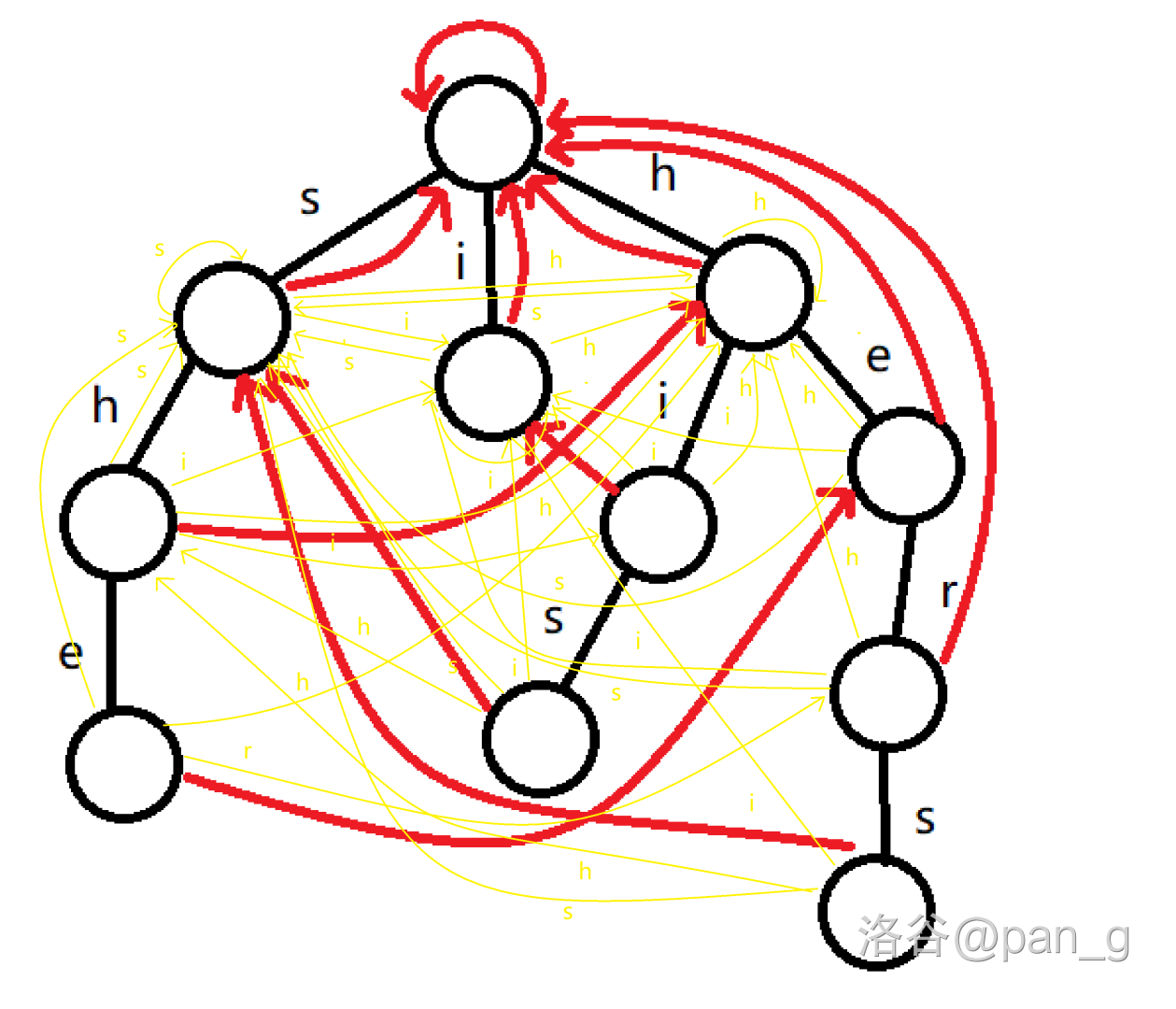
更加阔怕了,怎么回事?
我们对文本串进行遍历,即 p \leftarrow \delta(p, t_i) ,然后不断地跳 \operatorname{fail} 指针,直到 S 状态,最后将经过的且存在单词的状态标记。
经过一通简单分析,可以发现这个方案的时间复杂度并不优,是 O(\sum |s_i| + |t|\max |s_i|) 的。
考虑优化,观察到 \operatorname{fail} 的指针一定指向深度较低的点,所以一定不会成环,而刨去初始状态之外,每个点都是只有一个指向,所以如果仅保留除 S 外的所有 \operatorname{fail} 指针,得到的一定是一棵树。
流行的一共有两种优化方案,一种是拓扑排序,就是遍历到一个点打一个标记,再用拓扑序上递推或 DP 的方式传到所有节点;还有一种是 DFS ,两者本质相同,不过多赘述。
到这里,可以将 luogu 上的三个模板做一下。
更常见的 AC 自动机主要是用于 AC 自动机上 DP ,省选里面肯定见到 AC 自动机,肯定是要带 DP 的,这种形式在上述优化中提到了,例题暂时还没做【再挖一坑】。